Semantics of Knowledge Graphs
Wouter Beek (wouter@triply.cc)

Part I: Formal Meaning
Formal meaning
Meaning is formalized with 2 functions:
- Interpretation function ($I$)
- From terms (syntax) to resources and properties (semantics).
- Extension function ($Ext$)
- From properties (semantics) to pairs of resources (semantics).
The combination of an specific interpretation function and a specific extension function is a model ($M$).
Meaning of terms

The interpretation of a node is the resource it refers to.
The interpretation of a predicate term is the property it denotes.
The extension of a property is the collection of pairs of resources that are connected by that property.
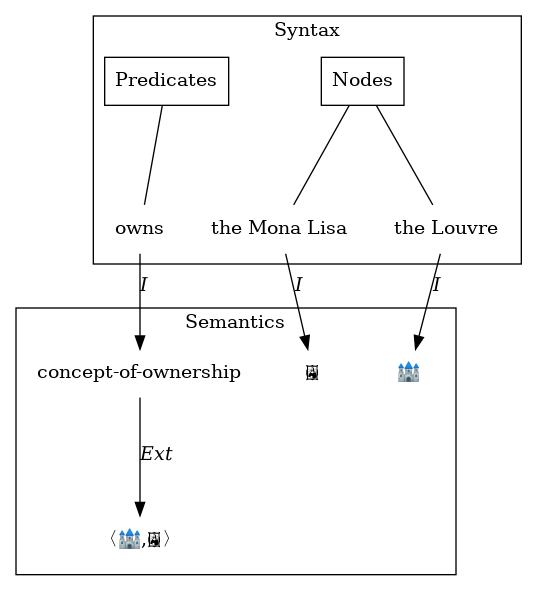
Meaning of terms: example

Meaning of sentences: Truth-conditional Semantics
To understand what a sentence means is to know what is the case if it would be true. (One can understand a sentence, without knowing whether it is true.)
Truth of a triple
$$\langle s,p,o \rangle \text{ is true} \iff \langle I(s),I(o) \rangle \in Ext(I(p))$$
$$\langle \text{the Louvre}, \text{owns}, \text{the Mona Lisa} \rangle \text{ is true} \iff$$ $$\langle I(\text{the Louvre}), I(\text{the Mona Lisa}) \rangle \in Ext(I(\text{owns})) \iff$$ $$\langle 🏰, 🖼 \rangle \in Ext(\text{concept-of-ownership}) \iff$$ $$\langle 🏰, 🖼 \rangle \in \{ \langle 🏰, 🖼 \rangle \}$$ ✓
$$\langle \text{the Mona Lisa}, \text{owns}, \text{the Louvre} \rangle \text{ is true} \iff$$ $$\langle I(\text{the Mona Lisa}), I(\text{the Louvre}) \rangle \in Ext(I(\text{owns})) \iff$$ $$\langle 🖼, 🏰 \rangle \in Ext(\text{concept-of-ownership}) \iff$$ $$\langle 🖼, 🏰 \rangle \in \{ \langle 🏰, 🖼 \rangle \}$$ ❌
Meaning of a triple
The meaning of a triple is the set of models in which the triple is true.
Meaning of a graph
The meaning of a graph is the set of models in which the triples in the graph are true.
Open World Assumption (OWA) & Closed World Assumption (CWA)
Difference between OWA and CWA
- Database
- “Apples are green.”
- Question
- “Are apples delicious?”
- CWA answer
- “No.”
- OWA answer
- “I don't known.”
Why does the SW need OWA?
In a local database, we can assume that we always have full access to all the relevant data.
On the web, we may not always have access to all the relevant data all the time.
Example of OWA
- I(the Louvre) = 🏰
- I(the Mona Lisa) = 🖼
- Ext(I(owns)) = {〈 🏰,🖼〉}
- Ext(I(exhibits)) = {〈 🏰,🖼〉}
With CWA, owning and exhibiting would have the same meaning. With OWA, they may still be different.
- I(owns) = concept-of-ownership
- I(exhibits) = concept-of-exhibiting
Corner case example (1/2)
rdfs:Class a rdfs:Class.- I(
rdfs:Class) = 🐕 - I(
a) = 🐘 - Ext(🐘) = {〈🐕,🐕〉,…}
This statement cannot be expressed with CWA, due to the
axiom of regularity: ∀x (x≠∅ → ∃y∈x(x∩y=∅))
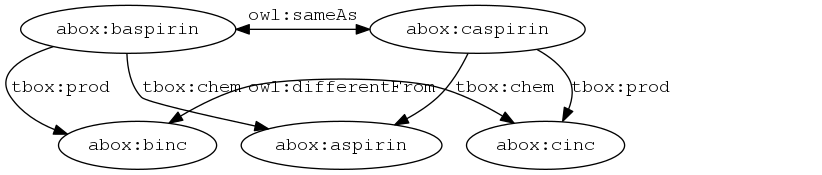
Corner case example (2/2)
owl:sameAs owl:sameAs owl:sameAs.- I(
owl:sameAs) = ~ - Ext(~) = {〈~,~〉,…}
〈owl:sameAs,owl:sameAs,owl:sameAs〉is true iff〈I(owl:sameAs),I(owl:sameAs)〉∈ Ext(I(owl:sameAs))
Notice that an RDF graph is a special kind of graph, i.e., vertices and edges may overlap.
Instances belong to classes
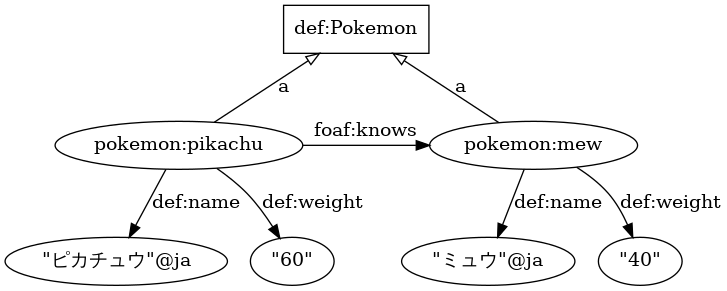
pokemon:mew a def:Pokemon;
def:name "ミュウ"@ja;
def:weight 40.
pokemon:pikachu a def:Pokemon;
def:knows pokemon:mew;
def:name "ピカチュウ"@ja;
def:weight 60.Domain & range
foaf:knows rdfs:domain foaf:Person.
ex:john foaf:knows ex:mary.
=> ex:john a foaf:Person.foaf:knows rdfs:range foaf:Person.
ex:john foaf:knows ex:mary.
=> ex:mary a foaf:Person.SPARQL Algebra
SPARQL algebra
- Variables V
- Solution mapping μ:V → T
- Pattern instance mapping P := μ ∘ σ
- Basic Graph Pattern (BGP) x
- μ is a solution for x from G, if (∃P)(P(x) ⊆ G and μ is the restriction of P to V(x)
Example 1
Dataset
prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>
rdfs:Class a rdfs:Class.BGP
?x a ?y.
Solution μ =
{(?x,rdfs:Class),(?y,rdfs:Class)}
Example 2
Dataset
prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>
rdfs:Class a rdfs:Class.BGP
_:1 a _:2.- Solution μ = ∅
-
σ = {(
_:1,rdfs:Class), (_:2,rdfs:Class)}
Alternative semantics for owl:sameAs
Definitions of identity
Indiscernibility of identicals (Leibniz's Law)
$$a = b \rightarrow (\forall \phi \in \Psi)(\phi(a) = \phi(b))$$
Identity of indiscernibles
$$(\forall \phi \in \Psi)(\phi(a) = \phi(b)) \rightarrow a = b$$
Equivalence relation
Identity is the smallest equivalence relation
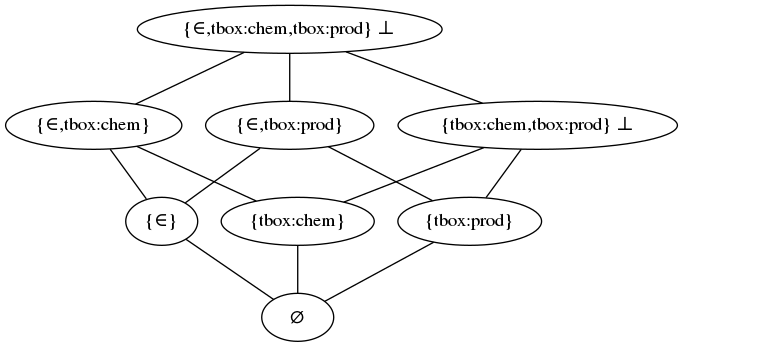
Formal Concept Analysis (FCA)
Context: instances (X), properties (Y), mapping (m)
$$X' \,:=\, \{ y \in Y \,\vert\, (\forall x \in X)(m(x,y)) \}$$
$$Y' \,:=\, \{ x \in X \,\vert\, (\forall y \in Y)(m(x,y)) \}$$
Formal concept 〈X,Y〉: X'=Y and Y'=X
Thank you for your attention!
- WWW: demo.triply.cc
- Email: wouter@triply.cc
- Twitter:
@WGJBeek
